43 递归的思想与应用(上)
从这节开始我们又要开启一个新的篇章了,我们将学习递归以及递归的应用,当然有人可能会问,说递归算是数据结构里面的内容吗?其实呢从严格意义上来说,递归并不是《数据结构》里面的内容,但是由于在我们后续学习中,比方说排序里面,比方说树里面都会借助于递归来进行研究,所以说我觉得我们有必要来系统的看看递归究竟是什么?系统的学学递归如何使用。
递归是一种数学上分而自治的思想
-
将原问题分解为规模较小的问题进行处理
- 分解后的问题与原问题的类型完全相同,但规模较小
- 通过小规模问题的解,能够轻易求得原问题的解
-
问题的分解是有限的(递归不能无限进行)
- 当边界条件不满足时,分解问题(递归继续进行)
- 当边界条件满足时,直接求解(递归结束)
-
递归模型的一般表示法
-
递归在程序设计中的应用
- 递归函数
- 函数体中存在自我调用的函数
- 递归函数必须有递归出口(边界条件)
- 函数的无限递归将导致程序崩溃
- 递归函数
-
递归思想的应用
-
求解:Sum(n) = 1+2+3+...+n
-
编程实验(一)
-
递归求和
unsigned int sum(unsigned int n){
if(n==1) return 1;
return n+sum(n-1);
}
递归的思想与应用(二)
-
斐波拉契数列
- 数列自身递归定义:1,1,2,3,5,8,13,21,...
编程实验(二)
-
斐波拉契数列
unsigned int Fibonacci(unsigned int n){
if(n<3) return 1;
return Fibonacci(n-1)+Fibonacci(n-2);
}
递归的思想与应用(三)
-
用递归的方法编写函数求字符串长度

编程实验(三)
-
求字符串长度
unsigned int strlen(const char *s){
if(*s=='\0') return 0;
return strlen(s+1)+1;
}
小结
- 递归是一种将问题分而治之的思想
- 用递归解决问题首先要建立递归的模型
- 递归解法必须要有边界条件,否则无解
- 不要陷入递归函数的执行细节,学会通过代码描述递归问题
44 递归的思想与应用(中)
递归的思想与应用(一)
-
单向链表的转置
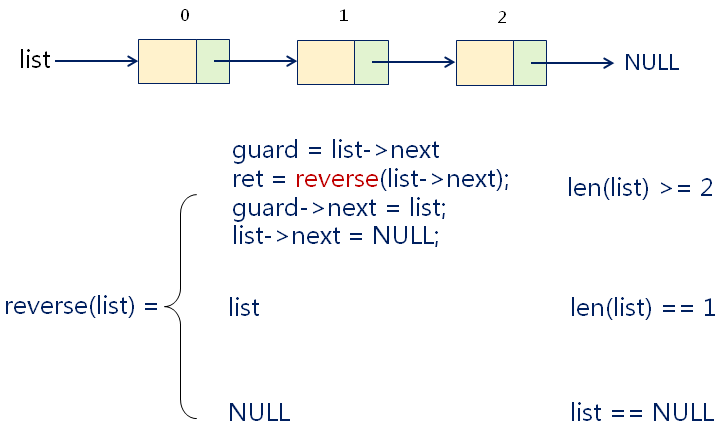
编程实验(一)
-
单向链表的转置
Node* reverse(Node* list){
if(list == nullptr)
return nullptr;
else if(list->next==nullptr)
return list;
else {
auto guard = list->next;
auto ret = reverse(list->next);
guard->next = list;
list->next = nullptr;
return ret;
}
}
递归的思想与应用(二)
-
单向排序链表的合并
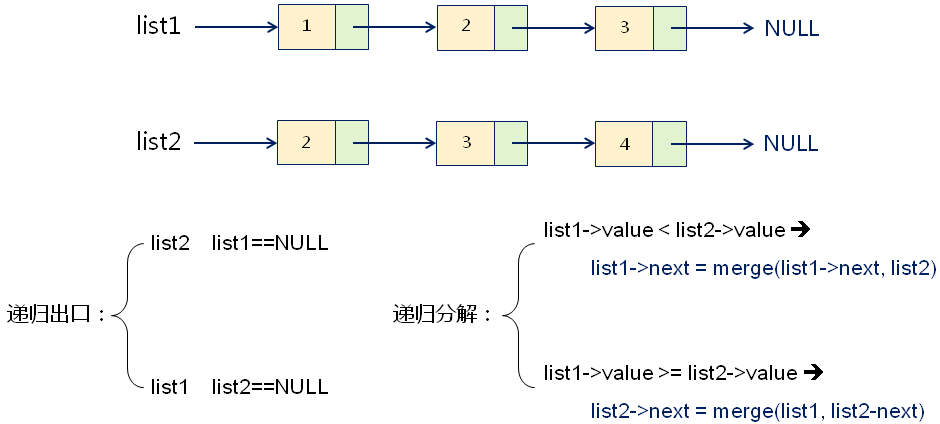
编程实验(二)
-
单向排序链表的合并
Node* merge(Node *list1,Node *list2){
if(list1 == nullptr)
return list2;
else if(list2 == nullptr){
return list1;
} else {
if(list1->value<=list2->value){
list1->next = merge(list1->next,list2);
return list1;
} else {
list2->next = merge(list1,list2->next);
return list2;
}
}
}
递归的思想与应用(三)
-
汉诺塔问题
- 将木块借助B柱由A柱移动到C柱
- 每次只能移动一个木块
- 只能出现小木块在大木块之上
-
汉诺塔问题分解
- 将n-1个木块借助C柱由A柱移动到B柱
- 将最底层的唯一木块直接移动到C柱
- 将n-1个木块借助A柱由B柱移动到C柱
编程实验(三)
-
汉诺塔问题求解
void HanoiTower(int n,char a, char b,char c){
if(n>1){
HanoiTower(n-1,a,c,b);
std::cout<<a<<"->"<<c<<std::endl;
HanoiTower(n-1,b,a,c);
}else {
std::cout<<a<<"->"<<c<<std::endl;
}
}
递归的思想与应用(四)
-
全排列问题
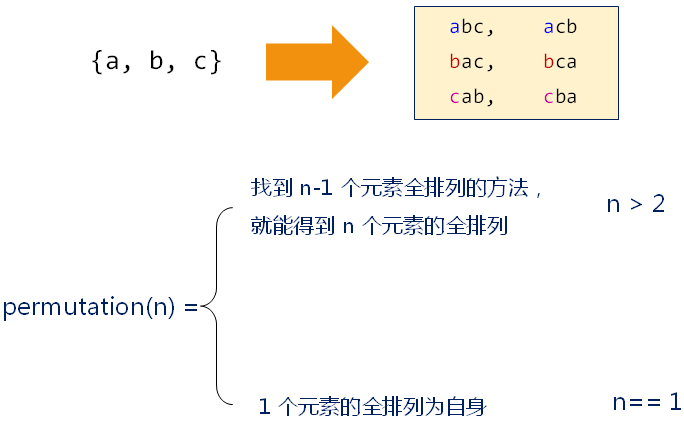
编程实验(四)
-
全排列的递归解法
void permutation(char *s,char *e){
if(*s!='\0'){
auto length = strlen(s);
for (size_t i =0;i<length;i++) {
std::swap(s[0],s[i]);
permutation(s+1,e);
std::swap(s[i],s[0]);
}
} else {
std::cout<<e<<std::endl;
}
}
递归的思想与应用(五)
- 小提示 递归还能用于需要回溯穷举的场合......
45 递归的思想与应用(下)
递归的思想与应用
-
函数调用过程回顾
- 程序运行后有一个特殊的内存区供函数调用使用(栈)
- 用于保存函数中的实参,局部变量,临时变量,等
- 从起始地址开始往一个方向增长(如:高地址->低地址)
- 有一个专用“指针”标识当前已使用内存的"顶部"
- 程序运行后有一个特殊的内存区供函数调用使用(栈)
-
程序中的栈区:一段特殊的专用内存区
-
实例分析:逆序打印单链表中的偶数结点
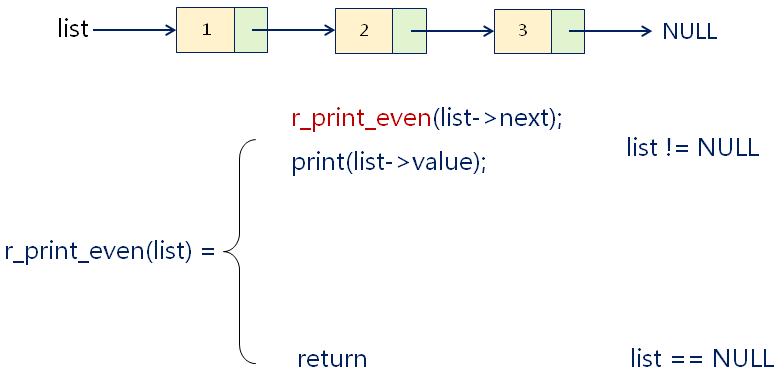
编程实验
-
函数调用栈分析
void r_print_even(Node* list){
} -
八皇后问题 在一个8x8的国际象棋棋盘上,有8个皇后,每个皇后占一格;要求皇后间不会出现相互“攻击”的现象(不能有两个皇后处在同一行、同一列或同一对角线上)。

-
关键数据结构定义:
-
棋盘:二维数组(10*10)
- 0表示位置为空,1表示皇后,2表示边界
-
位置:struct Pos;
struct Pos{
int x;
int y;
}; -
-
关键数据结构定义
- 方向 水平:(-1,0),(1,0) 垂直:(0,-1),(0,1) 对角线:(-1,1),(-1,-1),(1,-1),(1,1)
-
算法思路
- 初始化:j=1
- 初始化:i=1
- 从第j行开始,恢复i的有效值(通过函数调用栈进行回溯),判断第i个位置
- 位置i可放入皇后:标记位置(i,j),j++,转步骤2
- 位置i不可放入皇后:i++,转步骤a
- 当i>8时,j--,转步骤3
- 结束:
- 第8行可放入皇后
编程实验
-
八皇后问题的递归解法
小结
- 程序运行后的栈存储区专供函数调用使用
- 栈存储区用于保存实参,局部变量。临时变量,等
- 利用栈存储区能够方便的实现回溯算法
- 八皇后问题是栈回溯的经典应用